SOCIAL DISTANCING
View(s):Maths in Action 47
By R. N. A. de Silva
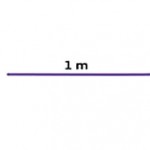
Social distancing helps limit opportunities of contact with infected people and contaminated surfaces during a period of a pandemic such as COVID-19. The World Health Organization has recommended 1 m of physical distance which many countries including Sri Lanka, have tried to maintain. Some countries have opted to have 2 m or 1.5 m physical distancing. 1 m can be considered as
an arm’s length.
Some people have come up with creative ideas in implementing this distance. A school in Zhejiang Province in China has produced one-metre hats using sticks, cardboard and balloons. Some people in Malviya Nagar, a locality in New Delhi, have started venturing out with an umbrella to help keep the distance. This helps as most umbrellas have a radius of 3 feet which is approximately 1 m.
Let us try to connect mathematics with social distancing patterns.
Most of the time we see people queuing one behind the other in a straight line, trying to have a gap of 1 m. How many people can be around you so that everybody is 1 m away
from each other?
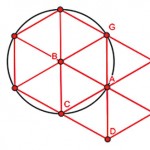
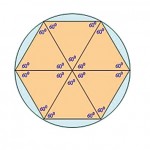
The best way to visualize this situation is to think of a circle of 1 m radius where you are at the centre. Because of the geometric properties of the circle, you can have six other people around you with 1 m gaps with each other, as shown in the figure.
Therefore, there are 7 people in this compound. Consider the centre as A and the vertex (corner) to the left of the centre as B. Now, if you draw a circle
with B as the centre, you can have
3 more people following social distancing guidelines, giving a total of 10. This is shown in the next figure.
Try adding one more circle and check the new total. Repeat this process to see what the total is, depending on the number of circles. You will notice that 3 are added with each new circle.
1 circle: 7 positions
2 circles: 10 positions
3 circles: 13 positions
circles: (3n + 4) positions.
This is the formula to obtain the number of positions given if there are n circles.
As an example, if you draw 10 circles,
you can have 34 positions.
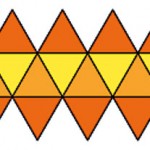
In the figure below, the circles are removed and also some of the outer lines are not drawn, as what is important are the vertices which are the positions. Count how many vertices are there.
If you were to include the circles,
how many do you think will be there?
Try to use the formula above to obtain
the answer.
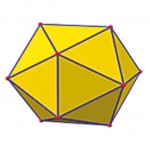
By the way, this is the net for forming a polyhedron called ‘Icosahedron’. By folding along the edges, an icosahedron can be constructed, as shown in the diagram. It has 20 equilateral triangle faces, 12 vertices and 30 edges.
It is interesting to see how mathematics helps us to make innovations with a simple idea and
bring in another dimension.